The Combined Gas Law

Since , If we change one of the variables, (P, V, n, or T) then one or more of the other variables must also change.  This leads to the equation  or if the number of moles stays the same .

Boyle's Law:

Boyle's Law examines the effect of changing volume on Pressure.  To isolate these variables, temperature must remain constant.  We can eliminate temperature from both sides of the equation and we are left with P₁V₁= P₂V₂

Sample Problem:  A piston with a volume of gas of 1.0 m³ at 100 kPa is compressed to a final volume of 0.50 m³.  What is the final pressure?

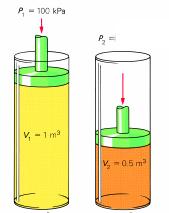
P₁ is 100 kPa

V₁ is 1.0 m³

V₂ is 0.50 m³

P₂ is unknown

P₁V₁= P₂V₂ becomes

Charles's Law

Charles's Law examines the effect of changing temperature on volume. To isolate these variables, pressure must remain constant.

 so Charles's law is

Sample problem: A piston with a volume of gas of 1.0 m³ at 273 K is cooled to a temperature of 136.5 K.   What is the final volume? (Assume pressure is kept constant.)

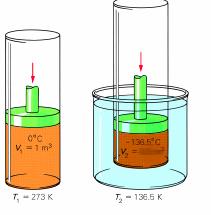
T₁ is 273 K

V₁ is 1.0 m³

V₂ is unknown

T₂ is 136.5 K

The solution becomes

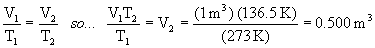
 Charles law Applet  See what happens when you increase temperature.  Increasing temperature __________ pressure.

GUY-LUSSAC'S LAW
Near the turn of the 19th century, Guy-Lussac investigated the relationship between pressure and temperature while the volume was held constant.  When the temperature goes up the pressure inside a rigid container also goes up.  For example, your car tires, when inflated, are essentially rigid, the volume will not change.  Did you notice that when the temperature goes up the pressure inside your tires also increases?

We can again use the combined gas law to quantify this relationship.

Sample Problem:   If your tire is two liters and the initial pressure is 2 atm, what is the final pressure when the temperature goes from 0 degrees celcius (273 K) to 100 degrees celcius (373 K)?

T₁ is 273 K
P₁ is 2 atm
P₂ is unknown
T₂ is 373 K

First, start with the combined gas law and cancel out the volumes because they do not change.

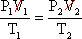
After removing the volumes,

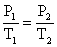
Rearranging the equation:
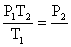 so the final pressure P2, is (2.00 atm)(373K)/(273 K) = 2.73 atm