(Biography at http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Broglie.html or http://www.chembio.uoguelph.ca/educmat/chm386/rudiment/tourquan/broglie.htm )
De Broglie looked at the results of the Einstein’s work where Einstein stated that energy, a wave, has particle like properties. De Broglie suggested that if light can behave like a matter, perhaps matter could behave like light. That is both light and matter have wave and particle-like properties. From the equation E=mc2 ,de Broglie derived the equation
![]()
where lambda is the wavelength, h is a constant (Plank’s constant), m is mass and v is the velocity of a moving particle. For most large objects, like me, my mass is large which makes my wavelength so small it is undetectable. For small particles such as electrons, the wavelength is important.
The proof for this hypothesis came in 1927 when Clinton Davisson and Lester Germer of Bell Labs saw an interference pattern when electrons were scattered by a nickel crystal. Notice the similarity of their particle experiment with the interference experiment with light described on page 206 of your textbook. (Figure 6-42.)
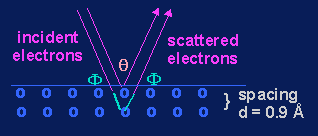 Davisson-Germer
Experiment (1927)
Davisson-Germer
Experiment (1927)
The upshot of this idea is that if electrons have wave-like properties, then only certain waves will “fit” for a given atom. The picture below shows a wave that firs and one that does not.
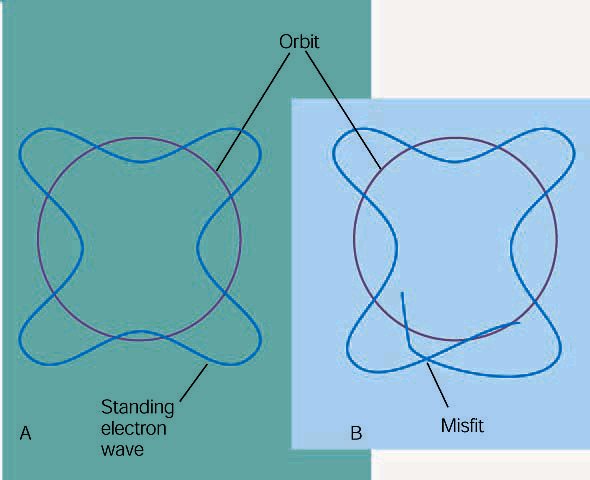
(A) A
schematic of de Broglie wave, where the standing wave pattern will just fit in
the circumference of an orbit. This is an allowed orbit. (B) This orbit does not
have a circumference that will match a whole number of wavelengths; it is not an
allowed orbit.
Your book does a nice job reconciling the Bohr model with the de Broglie theory. Notice in the picture below that each “orbit” of the Bohr model has a corresponding de Broglie wave.
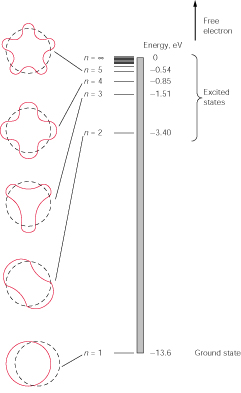
FIG. 8-15
Energy levels of the hydrogen atom. The energies are negative, which signifies
that the electron is bound to its nucleus.